a084.
NOI2001 Day1.2.反正切函数的应用
內容
反正切函数可展开成无穷级数，有如下公式
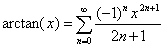(其中0 <= x <= 1) 公式(1)
使用反正切函数计算PI是一种常用的方法。例如，最简单的计算PI的方法：
PI=4arctan(1)=4(1-1/3+1/5-1/7+1/9-1/11+...) 公式(2)
然而，这种方法的效率很低，但我们可以根据角度和的正切函数公式：
tan(a+b)=[tan(a)+tan(b)]/[1-tan(a)*tan(b)] 公式(3)
通过简单的变换得到：
arctan(p)+arctan(q)=arctan[(p+q)/(1-pq)] 公式(4)
利用这个公式，令p=1/2,q=1/3，则(p+q)/(1-pq)=1，有
arctan(1/2)+arctan(1/3)=arctan[(1/2+1/3)/(1-1/2*1/3)]=arctan(1)
使用1/2和1/3的反正切来计算arctan(1)，速度就快多了。
我们将公式(4)写成如下形式
arctan(1/a)=arctan(1/b)+arctan(1/c)
其中a,b和c均为正整数。
我们的问题是：对于每一个给定的a（1 <= a <= 60000），求b＋c的值。我们保证对于任意的a都存在整数解。如果有多个解，要求你给出b+c最小的解。
使用反正切函数计算PI是一种常用的方法。例如，最简单的计算PI的方法：
PI=4arctan(1)=4(1-1/3+1/5-1/7+1/9-1/11+...) 公式(2)
然而，这种方法的效率很低，但我们可以根据角度和的正切函数公式：
tan(a+b)=[tan(a)+tan(b)]/[1-tan(a)*tan(b)] 公式(3)
通过简单的变换得到：
arctan(p)+arctan(q)=arctan[(p+q)/(1-pq)] 公式(4)
利用这个公式，令p=1/2,q=1/3，则(p+q)/(1-pq)=1，有
arctan(1/2)+arctan(1/3)=arctan[(1/2+1/3)/(1-1/2*1/3)]=arctan(1)
使用1/2和1/3的反正切来计算arctan(1)，速度就快多了。
我们将公式(4)写成如下形式
arctan(1/a)=arctan(1/b)+arctan(1/c)
其中a,b和c均为正整数。
我们的问题是：对于每一个给定的a（1 <= a <= 60000），求b＋c的值。我们保证对于任意的a都存在整数解。如果有多个解，要求你给出b+c最小的解。
輸入說明
输入文件中只有一个正整数a，其中 1 <= a <= 60000。
輸出說明
输出文件中只有一个整数，为 b+c 的值。
範例輸入
#1
1
範例輸出
#1
5
測資資訊：
記憶體限制：
512
MB
公開 測資點#0 (10%): 3.0s , <1K
公開 測資點#1 (10%): 3.0s , <1K
公開 測資點#2 (10%): 3.0s , <1K
公開 測資點#3 (10%): 3.0s , <1K
公開 測資點#4 (10%): 3.0s , <1K
公開 測資點#5 (10%): 3.0s , <1K
公開 測資點#6 (10%): 3.0s , <1K
公開 測資點#7 (10%): 3.0s , <1K
公開 測資點#8 (10%): 3.0s , <1K
公開 測資點#9 (10%): 3.0s , <1K
公開 測資點#0 (10%): 3.0s , <1K
公開 測資點#1 (10%): 3.0s , <1K
公開 測資點#2 (10%): 3.0s , <1K
公開 測資點#3 (10%): 3.0s , <1K
公開 測資點#4 (10%): 3.0s , <1K
公開 測資點#5 (10%): 3.0s , <1K
公開 測資點#6 (10%): 3.0s , <1K
公開 測資點#7 (10%): 3.0s , <1K
公開 測資點#8 (10%): 3.0s , <1K
公開 測資點#9 (10%): 3.0s , <1K
提示 ：
標籤:
出處:
NOI2001Day1第二题
[管理者：
liouzhou_101
(王启圣)
]
| 編號 | 身分 | 題目 | 主題 | 人氣 | 發表日期 |
|
沒有發現任何「解題報告」
|
|||||