b118.
TOI2008 5. 彩色區塊
內容
在一個平面上散佈有數個大小不一且色彩不同的矩形區塊；其中，每一個矩形區塊的色彩皆可用色彩三原色：紅、綠、藍(R, G, B)表示。例如紅色為(255,0,0)，綠色為(0,255,0)，黃色為(255,255,0)，而白色為(255,255,255)。倘若這些矩形區塊有互相重疊的現象發生，則此重疊區域的色彩R、G、B值，將分別為所重疊之矩形區塊的R、G、B平均值。亦即，若此重疊區域由k個矩形區塊重疊而成，且此k個矩形區塊之R、G、B值分別為(R1,G1,B1)，(R2,G2,B2)，…，(Rk,Gk,Bk)，則此重疊區域之色彩R、G、B值即為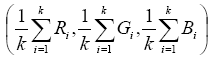
。(註：此平均值之計算方式，採「小數點以下無條件進位」方式計算。)
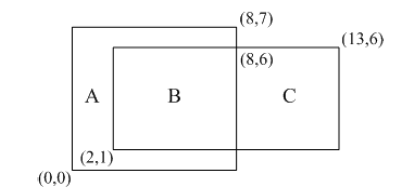
舉例來說，若平面上有兩個矩形區塊，其中第一個矩形區塊之對角線端點座標分別為(0,0)和(8,7)，第二個矩形區塊之對角線端點座標分別為(2,1)和(13,6)，則此兩個矩形區塊將產生一個重疊的矩形區域，其對角線端點座標分別為(2,1)和(8,6)，如下圖所示。倘若第一個矩形區塊之色彩R、G、B值為(100,100,100)，第二個矩形區塊之色彩R、G、B值為(200,200,200)，則此重疊的矩形區域之色彩R、G、B值可由上述公式計算得到為(150,150,150)。
輸入說明
輸入檔共計有N+1行的資料輸入。其中，輸入檔的第一行為一
個正整數N，代表平面上共散佈有N個矩形區塊(0<N<100)；輸入檔
中接下來的N行，每一行皆有7個以空白隔開的整數：第一和第二
個以及第三和第四個整數分別代表其中一個矩形區塊之對角線端點
的X與Y座標值(0≦X≦1000; 0≦Y≦1000)，第五、第六和第七個整
數分別代表此矩形區塊之色彩R、G、B值(0≦R≦255; 0≦G≦255;
0≦B≦255)。注意：在本題中，我們假設每一個矩形區塊在輸入檔中
只會被描述一次，且其對角線端點之X與Y座標值皆為正整數。
個正整數N，代表平面上共散佈有N個矩形區塊(0<N<100)；輸入檔
中接下來的N行，每一行皆有7個以空白隔開的整數：第一和第二
個以及第三和第四個整數分別代表其中一個矩形區塊之對角線端點
的X與Y座標值(0≦X≦1000; 0≦Y≦1000)，第五、第六和第七個整
數分別代表此矩形區塊之色彩R、G、B值(0≦R≦255; 0≦G≦255;
0≦B≦255)。注意：在本題中，我們假設每一個矩形區塊在輸入檔中
只會被描述一次，且其對角線端點之X與Y座標值皆為正整數。
輸出說明
請將分佈面積最大之色彩的R、G、B值，依序輸出於螢幕上。
注意：此色彩之分佈區域不一定為連續之區域；另外，每一組測試資
料只會有一種色彩擁有最大之分佈面積。
注意：此色彩之分佈區域不一定為連續之區域；另外，每一組測試資
料只會有一種色彩擁有最大之分佈面積。
範例輸入
#1
2 0 0 8 7 100 100 100 2 1 13 6 200 200 200 3 0 0 6 7 100 110 120 2 1 5 6 200 210 220 5 3 10 6 0 10 20
範例輸出
#1
150 150 150 100 110 120
測資資訊：
記憶體限制：
512
MB
公開 測資點#0 (100%): 20.0s , <1M
公開 測資點#0 (100%): 20.0s , <1M
提示 ：
標籤:
| 編號 | 身分 | 題目 | 主題 | 人氣 | 發表日期 |
|
沒有發現任何「解題報告」
|
|||||