d371.
3. Huffman 編碼中的編碼效能問題
內容
為了用0 與1 的位元串表示電腦中所需使用的符號,常見的編碼法可分為兩大類:固定長度編碼法與非固定長度編碼法。
固定長度編碼法指的是,將每個符號用相同長度的位元串表示。
例如,要以二進位的0 與1 位元串表示{a, b, c, d, e } 5個符號
每個符號最少需要以3 個位元來編碼成{000, 001, 010, 011, 100}。
但如果我們已知這些符號在多數資料中出現的頻率不同,就可用非固定長度編碼法更有效地表示這些資料
而Huffman 編碼法就是非固定長度編碼法中最常使用的方法。
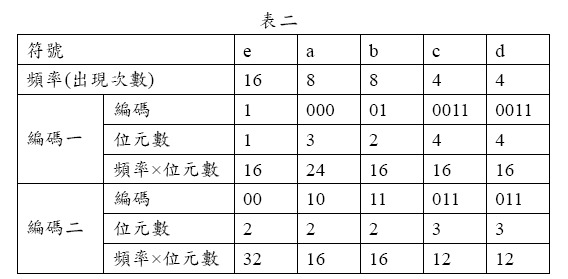
例如,已知{a, b, c, d, e}這5 個符號的出現頻率由大至小如表一所示。

則Huffman 編碼法利用建立二元樹的方式,首先將每個符號以一個自由節點(freenode)表示
這些自由節點的權重(weight)即是符號的頻率。
接著,從自由節點中找出權重最小的兩個節點,為這兩個節點做一個父節點,此父節點的權重則為這兩個子節點的權重和。
之後,將父節點加入自由節點的行列,並將兩個子節點從自由節點的行列中去除。
接著,重覆選取兩個權重最小的節點,造出父節點並更新自由節點的過程,直到最後只剩一個自由節點為止。
當得到這棵編碼樹後,我們就可以從二元樹的根結點(root node)開始往下走
每往左子樹(left subtree)走一層就給定一個位元的編碼0
每往右子樹(right subtree)走一層就給定一個位元的編碼1
依此方式逐層往下走並同時編碼直到走到葉節點(leaf node)為止。
圖一、二所示即為依表一頻率表所建造的不同Huffman 編碼樹。
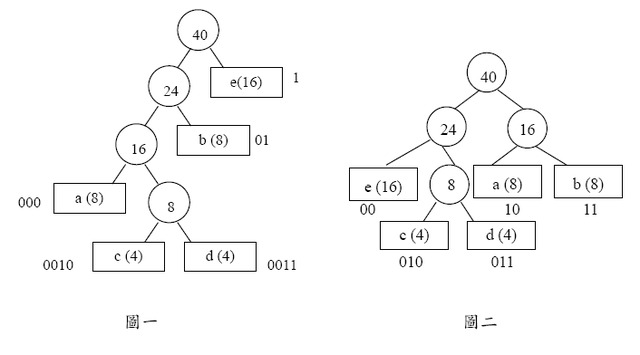
雖然圖一和圖二的編碼結果不同,但檢視其編碼效能,如表二所示,可發現這兩個編碼所得到的總位元數是相同的:
16+24+16+16+16+16=32+16+16+12+12=88。
請撰寫一個程式,根據已知的頻率表(尚未排序過),計算以Huffman 編碼後的總位元數。
輸入說明
第一行為一個整數n,代表共有幾個符號。(n<=2k,k 為正整數,1<k<=16)。
接下來的n 個數字代表這n 個符號的頻率,每個數字為介於1 與216 之間的正整數,每兩個數字以一個空格隔開。
輸出說明
對每一個輸入的頻率表,計算以Huffman 編碼後的總位元數。
範例輸入
#1
5 16 8 8 4 4
範例輸出
#1
88
測資資訊:
記憶體限制:
512
MB
不公開 測資點#0 (20%): 2.0s , <1K
不公開 測資點#1 (20%): 2.0s , <1K
不公開 測資點#2 (20%): 2.0s , <1K
不公開 測資點#3 (20%): 2.0s , <1M
不公開 測資點#4 (20%): 2.0s , <1M
不公開 測資點#0 (20%): 2.0s , <1K
不公開 測資點#1 (20%): 2.0s , <1K
不公開 測資點#2 (20%): 2.0s , <1K
不公開 測資點#3 (20%): 2.0s , <1M
不公開 測資點#4 (20%): 2.0s , <1M
提示 :
標籤:
| 編號 | 身分 | 題目 | 主題 | 人氣 | 發表日期 |
|
沒有發現任何「解題報告」
|
|||||