a069. NOI1999 Day2.1.棋盘分割 - 高中生程式解題系統

內容

将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

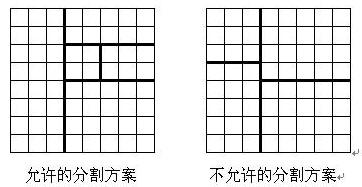
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的均方差最小。
均方差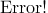

，其中平均值

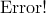，x_i为第i块矩形棋盘的总分。
请编程对给出的棋盘及n，求出O'的最小值。

輸入說明

第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

輸出說明

仅一个数，为O'（四舍五入精确到小数点后三位）。

範例輸入 #1

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

範例輸出 #1

1.633

測資資訊：

記憶體限制： 512 MB
公開測資點#0 (20%): 1.0s , <1K
公開測資點#1 (20%): 1.0s , <1K
公開測資點#2 (20%): 1.0s , <1K
公開測資點#3 (20%): 1.0s , <1K
公開測資點#4 (20%): 1.0s , <1K

提示：

標籤:

出處:

NOI 1999 Day2 第一题 [管理者： liouzhou_101 (王启圣) ]

編號	身分	題目	主題	人氣	發表日期
39290	qerpzzea@gma ... (賽希爾 cecill(陳宥穎))	a069		170	2024-02-01 23:26